Si vous ouvrez un dictionnaire et que vous cherchez la définition du mot "géométrie" vous trouverez une formule ressemblant à celle‑ci :

 "Branche des mathématiques qui étudie les propriétés de l'espace"

    Et en poursuivant, vous découvrirez une liste de spécialités comme : la géométrie analytique, euclidienne ou non, affine, pure, algébrique, différentielle, vectorielle, 3D et même virtuelle...

   Pourtant celle qui entoure notre vie, celle qui modèle notre monde, celle qui fit rayonner les artistes de tout temps, celle qui fit rencontrer les mathématiciens et les philosophes, celle qui aida les hommes à dialoguer avec leurs dieux, cette géométrie que l'on nomme sacrée est non citée. Cette science a‑t‑elle été évacuée de nos manuels scientifiques pour son côté ésotérique et insaisissable ? Ou tout simplement, notre perception du monde ne serait‑elle plus capable de décoder ce type de langage ?  

Les jardins de Versailles

Sommaire

   La Géométrie sacrée et les concepts de base

   Le Nombre d'Or et ses propriétés

   Les triangles sacrés

   Les mesures sacrées

   Le pentacle et le pentagone

   Le mètre et la coudée royale, des origines occultes

   La Géométrie sacrée dans l'affaire de Rennes

   Pourquoi ce thème et quel est son rapport avec Rennes‑le‑Château ?
Les passionnés et les chercheurs qui ont exploré l'affaire dans ses grandes lignes le savent bien. La géométrie est omniprésente dans les secrets du Razès et pour de multiples raisons. En voici quelques exemples :

   Je n'ai pas la prétention de dresser ici un panorama exhaustif de cette science qui est la Géométrie Sacrée. Il n'y en a pas. Je ne tomberais pas non plus dans de l'ésotérisme de pacotille. De nombreux auteurs ont déjà sombré sur cet écueil. Je me contenterai de fournir uniquement quelques clés indispensables à connaître, pour comprendre plus facilement les mécanismes, les règles et les contraintes que de nombreux artistes ont dû respecter dans leur art durant des siècles. Mais c'est aussi des notions qu'il faut connaître lorsque l'on aborde Rennes‑le‑Château et ses dérivés symboliques. Les codeurs ont utilisé cette forme de langage et pour s'en convaincre il suffit de survoler le Domaine de Saunière (voir la géométrie sacrée du Domaine)

   Si ceci nous paraît aujourd'hui complexe et peu connu, il faut savoir que la Géométrie Sacrée était pour nos ancêtres érudits, une forme de langage avec le divin tout à fait naturelle. Notre civilisation, hyper médiatisée et rationnelle, a malheureusement perdu ces concepts indispensables à la compréhension de nos racines et de notre monde...

   Mais mon objectif ambitieux est aussi de démystifier ce terme pompeux de "Géométrie Sacrée". Trop d'auteurs manipulent cercles et pentacles sans connaître exactement les symboles et les règles mathématiques qui y sont associés. Pire, dans l'esprit de beaucoup, la Géométrie Sacrée relève de l'impalpable, de l'occulte ou de la magie noire. C'est pourtant tout le contraire. Cette science décrit l'harmonie qui nous entoure et elle suit des règles mathématiques très précises.

   Nicolas Poussin, Maître en la matière, usa de cette science pour nous laisser dans les Bergers d'Arcadie un héritage merveilleux... On ne peut espérer soulever son voile, sans connaître les outils et les règles qu'il a utilisés.

Qu'est‑ce que la Géométrie Sacrée ?

Définitions

   Si l'on s'en tient à la définition d'un dictionnaire, la géométrie est la science mathématique qui étudie les relations entre points, droites courbes, surfaces et volumes dans l’espace. La géométrie devient Sacrée si on lui ajoute une dimension d'harmonie, des valeurs artistiques et une dimension divine... En d'autres termes, la Géométrie Sacrée utilise les concepts de la géométrie euclidienne simple, mais en mettant en relief l'harmonie universelle de notre monde.

   Mais attention,  le terme de Géométrie Sacrée englobe aujourd'hui tout et n'importe quoi, car même si elle possède l'attribut de Sacrée, elle n'en reste pas moins une science mathématique qui a ses règles strictes, ses théorèmes et ses axiomes. Trop d'auteurs utilisent cette géométrie pour donner une certaine consistance à des thèses plus ou moins ésotériques et à des constructions arbitraires.

   En fait il faudrait plutôt parler de Géométrie harmonieuse ou de mathématiques artistiques. Mais comme d'habitude, lorsqu'un sujet est peu connu ou mal maîtrisé car complexe, il est exploité et détourné pour mieux faire passer des idées très différentes. C'est tellement plus simple...

La voute étoilée de la cathédrale de Burgos

Ses origines et son domaine

   On retrouve la Géométrie Sacrée dans les temps les plus anciens et dans toutes les contrées du monde. Depuis l'aube du Ve millénaire av. J.‑C. l'homme s'est intéressé à cette science et ceci est nettement visible dans les restes archéologiques. Elle est intimement intégrée dans l'antiquité grecque, romaine, égyptienne, chinoise, aztèque, inca, mais aussi à notre moyen âge avec les bâtisseurs de cathédrale ou à l'époque de la renaissance occidentale. Elle touche non seulement l'architecture, mais aussi la peinture, la sculpture, l'orfèvrerie et même la littérature et la poésie. La Géométrie Sacrée étant harmonieuse, elle s'intègre dans toutes les formes de l'art et donc dans notre conscient et notre subconscient collectif.

Euclide d'Alexandrie
325 av. J.‑C.

   La Géométrie Sacrée englobe un nombre de domaines incalculables. En fait, sans le savoir et sans nous en apercevoir, nous baignons dans un monde régit par une mathématique harmonieuse et équilibrée. Le métier moderne appelée "Designer" n'est qu'une mutation de cet art adapté au monde moderne et aux contraintes économiques.

   Mais ce n'est pas tout. Cette science qui aurait pu être inventée par l'homme pour l'homme se retrouve en plus dans la nature. C'est la principale raison pour laquelle les anciens considéraient cette connaissance comme divine. Avant que l'homme ne découvre la Géométrie Sacrée, Dieu inventa la nature et l'harmonie...

   La géométrie Sacrée est donc la science descriptive qui met en lumière l'harmonie de notre monde. Elle est le reflet de notre conscience d'être. Mais cette géométrie ne représente qu'une infime partie du réel problème. Les anciens s'attachaient surtout à l'étude sur un plan à l'aide de la règle et du compas. Mais il faut savoir que les volumes ne sont pas non plus épargnés ni la dynamique, c'est à dire l'étude du mouvement des formes.

Qui utilisait la Géométrie sacrée ?

   Toutes les civilisations anciennes ont utilisé à des degrés différents cette science. Mais celle‑ci, demandant des connaissances très particulières en mathématiques et en géométrie, elle était réservée à une élite et donc à un pouvoir.

   Cette branche scientifique fut très vite élitiste et donc secrète. Celui qui domine cet art domine la création artistique et possède un puissant pouvoir sur les autres. Il faut donc considérer deux groupes : ceux qui l'utilisèrent comme les bâtisseurs de cathédrale, et ceux qui en avaient une connaissance approfondie comme Nicolas Poussin ou Léonard de Vinci...

Le Grand Architecte créant le Ciel et la Terre à l’aide du grand compas
(Bible de Vienne du XIII^e siècle)

   Aujourd'hui elle est toujours utilisée, mais souvent sans connaître les fondements symboliques qu'elle véhicule. Par exemple le Nombre d'Or est très connu dans les métiers de l'art, mais qui sait ce qu'est un Triangle divin ou combien vaut une coudée royale ? Se rappelle‑t‑on du génial Fibonacci ? Sait‑on que le retrouve le Nombre d'Or même dans notre ADN ?

Gravure maçonnique

Pourquoi utilisait‑on la Géométrie Sacrée ?

   Paradoxalement, même si l'on considère aujourd'hui que nos lointains ancêtres maîtrisaient les sciences de la terre comme l'astronomie, à des niveaux de connaissance qui nous étonnent encore aujourd'hui, il est certain qu'ils ne disposaient pas de la puissance de calcul qu'un architecte peut disposer aujourd'hui.

   De même tous les outils mathématiques modernes comme le calcul matriciel, vectoriel ou intégral, étaient inconnus. La géométrie offre un moyen simple de construire des chefs‑d'œuvre à l'aide d'outils simples et adaptés. Le compas en est certainement le plus bel exemple.

   Le fait d'utiliser la Géométrie Sacrée introduit  donc dans la réalisation une dimension harmonieuse, proche de la nature et donc divine... Mais c'est aussi un moyen souvent utilisé pour passer un ou plusieurs messages symboliques, seulement compris par les initiés. Utiliser la géométrie sacrée c'est entrer en communication avec Dieu et conserver un niveau de confidentialité très élevé.

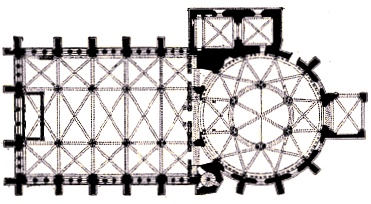
Plan de l'église du Temple à Londres

Pourquoi nos ancêtres ont‑ils tant vénéré cette science ?

   Toutes les anciennes civilisations ont considéré la Géométrie Sacrée comme une science divine. De plus étant présente dans la nature, elle participe à l'équilibre de notre vie matérielle. On comprend alors d'où provient cette expression "Dieu est partout et le créateur de toute chose". En effet la moindre feuille d'un arbre ou le plus petit coquillage respecte les lois mathématiques dorées et donc divines.

   La Géométrie Sacrée peut donc être considérée comme un langage  universel, rigoureux et harmonieux. L’univers tout entier est construit selon une harmonie parfaite. Les orbites des planètes autour du soleil sont structurées par des proportions très précises. Mais nous retrouvons aussi les mêmes concepts dans les cristaux, les plantes, les animaux et le corps humain.  

   Mais comme toute science du progrès génère ses travers, la géométrie sacrée a drainé au fil des siècles, des courants de pensée plus ou moins ésotériques qui ont fait naître différentes sociétés secrètes. La géométrie est la base sur laquelle s'est construite la franc‑maçonnerie. Le plus amusant est que très certainement les nombreux membres de ces sociétés n'avaient aucune connaissance dans cette science qui demande des études scientifiques approfondies.     

Les pyramides de Gizeh en Égypte ‑ L'expression même du Nombre d'Or

Un sujet complexe

   Tout le monde a pu contempler les mille et une étude des Bergers d'Arcadie noyées sous des cercles et des pentacles... Mais très peu se hasardent à faire des démonstrations. Il est très facile de jouer du compas, mais il est beaucoup moins évident d'établir des règles, des démonstrations et des postulats.

   C'est pour ceci que Nicolas Poussin reste incompris. Si aujourd'hui tout le monde est convaincu de la dimension géométrique extraordinaire de ses tableaux, personne ne sait expliquer sa méthode de construction ni les règles qu'il s'imposait. Pire, on ne sait même pas, malgré une biographie très complète, comment et par qui exactement il a pu acquérir une telle connaissance réservée à des initiés.

   Car le sujet est paradoxal. Alors qu'un grand nombre d'experts vous expliqueront qu'il n'y a aucun mystère dans ce tableau de Poussin, aucun ne saura vous expliquer comment il a élaboré cette composition rigoureuse et pourquoi.

Restons humbles

   La Géométrie Sacrée offre des outils permettant de comprendre les règles de construction que s'imposaient les artistes. Mais en aucun cas elle permet de comprendre le ou les messages véhiculés car il faut lui ajouter une  sémantique. Pour donner une analogie, la Géométrie Sacrée est comparable à la syntaxe et l'allégorie à la sémantique. Pour comprendre un texte, il faut maîtriser sa syntaxe et sa sémantique. Dans un tableau de la renaissance, ou dans l'architecture d'une cathédrale, il faut maîtriser sa géométrie harmonieuse et son contexte symbolique.

   Il aussi reconnaître que dans le cas de Nicolas Poussin, si nous disposons aujourd'hui de quelques notions de Géométrie Sacrée, le contexte sémantique des Bergers d'Arcadie est un autre problème.  Il faut donc rester humble devant le maître des Andélys.

Les concepts de base

Au tout début, il y a le cercle et un centre

   Le cercle est une forme à la fois simple et complexe. Mais comment les anciens l'on découverte ? Peut‑être tout simplement en observant un caillou qui tombe dans l'eau. Le choc de la surface crée alors une onde formant des cercles concentriques. Les feuilles mortes qui flottent à la surface se soulèvent pour laisser passer l'onde, mais elles ne s'écartent pas du centre.

   Nous avons alors un premier concept : le caillou définit un centre qui est un point et les cercles naissent à partir de ce point.

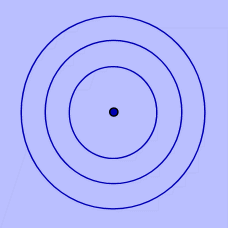
Cercles concentriques

Le centre est vu comme l'origine, la création de toute chose, le départ vers le multiple, l'endroit d'où l'esprit va rayonner. Le centre est Dieu

Le cercle est le monde spirituel créé à partir du centre, le ciel, la transcendance, l'éternité, l'Aura de Dieu. Les ronds dans l'eau bougent dans le temps. Le cercle c'est aussi le temps qui passe ou l'éternel recommencement. Les feuilles ne s'éloignent pas mais bougent sur place. Le monde spirituel enveloppe toute chose sans la perturber...

Puis vient le carré...

   Le carré est la forme la plus simple en géométrie et ses propriétés sont évidentes. Construit sur 4 droites , il symbolise l'équilibre et la rationalité.

   Le carré intervient dans de nombreuses figures géométriques comme un élément de base nécessaire à la construction de formes complexes.

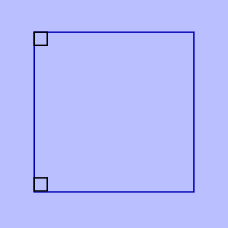
Le carré, une forme rigide

Le carré représente la stabilité, l'équilibre et le rationnel. Construit sur 4 piliers, il est solide et ses 4 coins sont associés aux 4 éléments naturels : eau, air, feu, terre. Le carré représente l'univers rationnel qui nous entoure.

La croix, un élément de liaison

   La croix apparaît par l'intersection de 2 droites. Mais c'est aussi cet élément qui aide à la construction géométrique. Elle permet par exemple de relier le cercle au carré mais aussi le point.

   Tracer une croix est le procédé géométrique élémentaire permettant de faire apparaître un point. Boudet l'a semble t‑il bien compris.

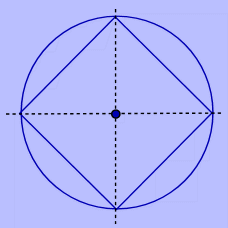
Le carré dans le cercle

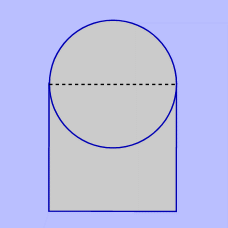
L'arc de triomphe romain

La croix met en relation le carré, le cercle et le point et donc établie une relation entre notre monde rationnel et Dieu.

Elle indique l'orientation, mais aussi la liaison entre le monde spirituel (le cercle), l'univers rationnel (le carré) et le point (Dieu). C'est aussi la liaison entre le ciel (le cercle) et la terre (le carré), entre le temps (le cercle) et l'espace (le carré), entre l'homme (le carré) et Dieu (le point).

La croix celtique est typiquement un bon exemple d'application mais on trouve aussi cette association dans l'arc de triomphe romain.

La croix est associée au chiffre 5 (4 coins du carré et le centre du cercle)

La croix celtique de Boudet
Dans l'église de Rennes‑le‑Château

Croix gravée dans un cercle
Croix celtique du VII^e siècle
Chapelle Scotts en Irlande

Les nombres constructibles

   Un nombre est dit constructible si un procédé par la règle et le compas permet de construire une longueur égale à sa valeur. Dans l'antiquité, les mathématiciens ne pouvaient utiliser que la droite et le cercle pour élaborer leurs théories et leurs démonstrations. Ceci revient à dire qu'ils ne pouvaient concevoir que l'univers rationnel (le carré) et le divin (le cercle)

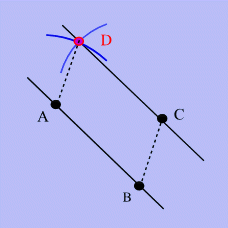
Exemple de construction
d'un parallélogramme

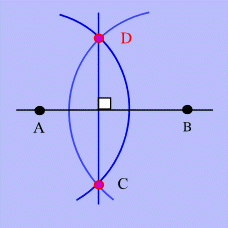
Exemple de construction
d'une perpendiculaire

   Un parallélogramme peut être construit par 3 points quelconques ABC. Le 4^e point D est l'intersection de 2 cercles, l'un de centre A et de rayon BC, l'autre de centre C et de rayon AB. Le point D est dit constructible.

   Une perpendiculaire se construit par 2 points quelconques AB. Les points C et D sont les intersections de 2 cercles, l'un de centre A et l'autre de centre B

Les nombres constructibles peuvent être additionnés (somme de 2 segments), soustraits, multipliés (par le théorème de Thalès sur les proportions) ou divisés.

On peut même extraire une racine carrée par le théorème de Pythagore.

Il suffit de tracer un cercle de diamètre AB tel que AB soit la valeur dont on veut calculer la racine carrée. Selon la propriété d'un triangle inscrit dans un demi‑cercle, ce triangle est rectangle en C.
On a donc par le théorème de Pythagore :

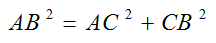
Plaçons le point H tel que la perpendiculaire à AB passe par C. Si AH = 1 on a :

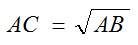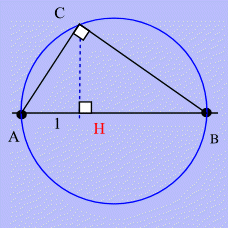
Extraction d'une racine carrée

La quadrature du cercle

   La quadrature du cercle est un problème classique qui fut longtemps posé comme une énigme par tous les mathématiciens. La question est de trouver une méthode géométrique basée sur la règle et le compas permettant de construire un carré de même surface (ou de même périmètre) qu'un cercle donné.

   Ce problème fait partie des 3 grands sujets mathématiques de l'antiquité que sont aussi la trisection d'un angle et la duplication d'un cube.

   On trouve dans un ancien document "le Papyrus Rhind" (1650 av. J.‑C.) l'exposé d'une solution approximative. Anaxagore de Clazomènes fut le premier grec qui étudia l'énigme. Plus tard Grégoire de Saint‑Vincent (1584‑1667), jésuite et mathématicien, écrivit un ouvrage de mille pages sur le sujet, mais sans le résoudre. En 1837, Pierre‑Laurent Wantzel travailla sur les problèmes impossibles à résoudre à la règle et au compas. Et en 1882, Ferdinand Von Lindermann démontra la transcendance de π ce qui permit avec les travaux précédents de démontrer l'absence de solution.  

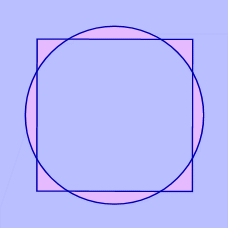
La quadrature du cercle
Le cercle et le carré ont la même aire

   Nous savons aujourd'hui que la règle et le compas ne suffisent pas pour créer une quadrature. Il faut utiliser d'autres outils comme la spirale d'Archimède.

   La spirale d'Archimède est la courbe obtenue par un point qui se déplace uniformément selon une droite en rotation uniforme autour d'un point. Le sillon de nos anciens disques vinyles est un bon exemple... Cette courbe peut être construite mécaniquement.

   La construction d'une quadrature du cercle nécessite la mise en œuvre de la racine carrée de π. Or, seuls les nombres constructibles peuvent être tracés à la règle et au compas.

   La quadrature du cercle est une opération fondamentale en Géométrie Sacrée puisqu'elle consiste à passer du monde spirituel (le cercle) au monde terrestre (le carré) et vice versa en passant par la croix. Cette relation géométrique, insoluble par la règle et le compas, mais établie mathématiquement, représente un pont entre le cercle, son centre et le carré, et donc entre Dieu et les hommes. Autant dire qu'elle a revêtu pour les anciens une opération tout à fait privilégiée et divine.

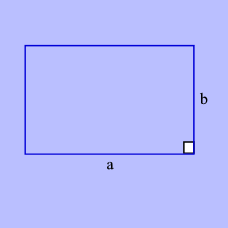
Le Rectangle d'Or

   Sa forme "parfaite" est étrangement liée au Nombre d'Or. Il est une des plus belles démonstrations de ce que nous jugeons de beau et harmonieux. Si vous demandez autour de vous de dessiner un rectangle équilibré et esthétique vous verrez que la moyenne des proportions dessinées tend vers le Rectangle d'Or, c'est à dire :

a / b = φ (Phi) = 1,6180...

φ étant le Nombre d'Or

Le Nombre d'Or, nombre divin

   La géométrie sacrée est rythmée par un nombre exceptionel : le Nombre d'Or. Ce nombre vénéré par les artistes et les architectes est indissociable de la nature. Comme nous le verrons plus loin, ses propriétés sont innombrables. Il est noté φ (Phi) et c'est un irrationnel qui vaut :

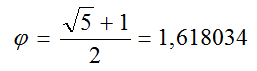
La suite page suivante