|
|
Si vous
ouvrez un dictionnaire et que vous cherchez la définition du
mot "géométrie" vous trouverez une formule ressemblant à
celle‑ci :
"Branche des mathématiques qui étudie les propriétés de l'espace"
Et en poursuivant, vous découvrirez une liste de spécialités
comme : la géométrie analytique, euclidienne ou non, affine, pure,
algébrique, différentielle, vectorielle, 3D et même virtuelle...
Pourtant celle qui entoure notre vie, celle qui modèle notre
monde, celle qui fit rayonner les artistes de tout temps, celle
qui fit rencontrer les mathématiciens et les philosophes, celle
qui aida les hommes à dialoguer avec leurs dieux, cette
géométrie que l'on nomme sacrée
est non citée. Cette science a‑t‑elle été évacuée de nos manuels
scientifiques pour son côté ésotérique et insaisissable ? Ou
tout simplement, notre perception du monde ne serait‑elle plus
capable de décoder ce type de langage ?
|

Les jardins de Versailles |
|
L'énigme de Rennes nous rappelle malgré tout
l'importance de la Géométrie sacrée et son caractère
incontournable. Car elle est tout simplement l'une des disciplines qu'il faut
maîtriser si l'on veut espérer comprendre et décoder certaines
pistes.
 |
|
Après, le carré et le cercle, la forme
géométrique la plus simple qui vient à l'esprit est
le
triangle. Nous avons tous
appris en géométrie euclidienne qu'il existe trois types
de
triangles remarquables :
 Le triangle rectangle :
L'un des angles est droit (90°)
Le triangle rectangle :
L'un des angles est droit (90°)
 Le triangle isocèle : Il a
2 côtés de même longueur
Le triangle isocèle : Il a
2 côtés de même longueur
 Le triangle équilatéral :
Il a 3 côtés de même longueur
Le triangle équilatéral :
Il a 3 côtés de même longueur
En fait, il existe d'autres triangles
ayant des caractéristiques tout aussi intéressantes et que
l'on retrouve dans la peinture, dans
l'architecture, ou dans les lieux sacrés. On parle alors de
Triangles Sacrés, dorés ou harmoniques.
Le triangle est représenté en hébreu "h"
(sans doute en relation avec les trois Hiram qui ont aidé à
construire le Temple de Salomon) ou par le chiffre "5". Sa
première interprétation est le symbole de Dieu ou du Grand
Architecte de l'univers qui est associé au triangle
équilatéral, symbole de perfection et que l'on l'appelle aussi le
"delta rayonnant".
|
|
Contrairement au carré ou
au rectangle qui représente notre
environnement matériel,
le triangle
est un symbole spirituel...
On le
trouve énormément dans l'architecture
sous forme de toiture, fronton,
charpente... C'est aussi le symbole de
la Chrétienté et de la Trinité (Père,
Fils et Saint Esprit). |
|
Le Triangle d'Or
Le
Triangle d'Or
est un triangle rectangle ABC possédant 2
côtés adjacents à l'angle droit de longueur
1
et
√φ
et un côté opposé de longueur
φ
Son périmètre est donc
égal à 1 +
√φ +
φ
Ceci provient d'une propriété
remarquable du Nombre d'Or qui est :
φ2
=
φ
+ 1
et qui
simplifie la formule de Pythagore puisque selon son théorème
on a : φ2
=
(√φ)2 + 1
|

|
|
Le Triangle d'Or
est symbole de perfection et d'harmonie. C'est le prince des triangles sacrés, et on le trouve
superbement mis en scène dans
la
pyramide de Chéops.
|
|
Le Triangle d'Isis
(Triangle 345)
Le
Triangle d'Isis,
que l'on appelle aussi triangle de Pythagore ou triangle des
Bâtisseurs, est un triangle rectangle
possèdant trois côtés de longueur respective
3,
4
et
5
Il est la conséquence
d'une
propriété arithmétique remarquable :
52 = 32 + 42
|
 |
Pour les bâtisseurs de tous temps, il
fut un moyen très simple de construire un angle droit, des
perpendiculaires ou des parallèles,
puisqu'il suffit de respecter la règle
3, 4, 5 sur une
corde à nœuds ou sur un tracé avec un compas.
Le
Triangle
345 est connu au moins depuis les Babyloniens qui
l'utilisaient pour vérifier les angles droits à l'aide
d'une corde à 13 noeuds (triangle de l'arpenteur). La
corde à 13 noeuds espacés de 12 intervalles égaux peut
ainsi être utilisée au sol en enfonçant trois piquets de
manière à ce que les trois côtés du triangle fasse
3 + 4 + 5 = 12 intervalles
Où se cache le
Nombre d'Or dans un triangle 345 ? |
Pour faire
apparaître le Nombre d'Or dans un triangle d'Isis, il
est nécessaire de tracer l'une des bisectrices appelées,
la bisectrices dorées.
Pour cela, il
faut au préalable tracer le cercle inscrit au triangle.
Son centre détermine alors le point par lequel les
bisectrices doivent passer. Tracer ensuite la bisectrice
correspondant au sommet Hypothénuse / petit côté. La
section de la bisectrice située entre ce sommet et le
périmètre du cercle mesure :
2 x Nombre d'Or
|
 |
|
Le Triangle d'Or et le Triangle d'Isis sont
pratiquement équivalents
Le Triangle d'Or
et le Triangle d'Isis sont souvent confondus. Il existe
en effet une différence très minime entre eux.
Dans un
Triangle d'Or le
rapport de l'Hypoténuse sur le petit côté vaut par définition φ.
Or, dans un Triangle d'Isis, le rapport équivalent de l'Hypoténuse sur le petit côté vaut
5/3 = 1,666 ce qui est très proche de
1,618... |
|
Le triangle
du Rectangle d'Or
Le triangle du
Rectangle d'Or
est un triangle rectangle possédant 2
côtés adjacents à l'angle droit de longueur
1
et
φ
et un côté opposé de longueur
√(φ2
+ 1)
La formule de Pythagore donne ceci :
√(φ2+1)
2
=
φ2
+ 1
|

|
|
Chose étonnante,
tous les triangles de rectangle d'or (harmoniques) peuvent être construits à partir d'un
carré.
Pour construire un triangle
de rectangle d'or, il suffit
de tracer un carré de côté
1 et une droite partant de l'un des sommets au
côté opposé en le coupant au milieu au point I.
Ensuite on trace un cercle de centre I et passant par
le sommet du carré. On obtient alors le point
A. |
|
Le triangle du
Rectangle d'Or
peut aussi être construit, comme son nom l'indique, à partir d'un
rectangle d'or
et donc avec :
le petit côté =
1 et
le grand côté = φ
Il suffit ensuite de diviser le rectangle par sa diagonale.
En clair
le triangle du Rectangle d'Or est la moitié du Rectangle d'Or,
ce dernier étant divisé par la diagonale.
|
 |
|
Le Triangle de Chéops
Il tient son nom de sa forme
pyramidale que l'on retrouve dans le profil de
la pyramide de Chéops. C'est aussi le profil
naturel d'un tas de sable sortant par exemple d'un sablier.
Cette propriété était bien connue de toutes les
civilisations égyptiennes ou d'Amérique du Sud.
Le triangle de Chéops possède
deux
côtés de longueur
φ
et un côté de longueur
2. La hauteur est
√φ. Le triangle de Chéops est
formé par deux triangles d'or.
|

|
|
Le Triangle Divin
Très souvent utilisé pour représenter
Dieu, on le retrouve dans la peinture ou dans
l'architecture.
Le
Triangle Divin
possède un côté de longueur
φ
et deux côtés de longueur 1. Il est
facilement détectable puisqu'il possède également trois angles
justes de 108° et 36°
Il est aussi une composante importante
du
pentagone régulier avec
son angle de 108°,
ce qui confère au pentagone sa
propriété divine.
|

|
|
Le Triangle Sublime
Le
Triangle Sublime a été très
étudié par les disciples d'Euclide d'où son second nom
"Triangle d'Euclide". C'est un triangle isocèle
possédant deux côtés de longueur
φ
et un côté de longueur
1.
Dit autrement, un triangle est Sublime si le rapport de la
longueur du côté double à la longueur du côté base est le
Nombre d'or. Ce triangle est aussi
facilement détectable puisqu'il possède trois angles
justes de 72° et 36°
On le retrouve très facilement dans le
pentagone régulier
|

|
|
Le Triangle d'Argent
Le
Triangle d'Argent possède
deux
côtés de longueur
φ
et sa hauteur depuis l'angle de
144°vaut 1/2. Il est facilement détectable puisqu'il possède
trois angles justes de
144° et 18°
La longueur de sa base vaut :
 |

|
|
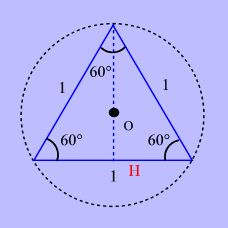
Le Triangle Equilatéral
Le
Triangle Equilatéral est le
roi des triangles. Son égalité en tout point est le symbole
même de l'harmonie et de l'équilibre.
C'est aussi un élément fondamental
dans le tracé d'autres formes harmonieuses comme
le pentacle ou l'étoile de
David.
Sa hauteur vaut :

|
|
|
Le Triangle des Bâtisseurs
Le Triangle des Bâtisseurs
(ou équerre des bâtisseurs)
possède deux côtés de longueur respective
1 et 2
(à ne pas confondre avec le
Triangle d'Isis que l'on appelle aussi triangle des
bâtisseurs)
Le Triangle des Bâtisseurs est comme
son nom l'indique, l'équerre des architectes. Tous les
triangles liés au Nombre d'Or ont une racine de 5 cachée dans
la hauteur ou sur un côté. Il s'inscrit aussi dans un double
carré.
|

|
|
Le Triangle Double carré
Le
Triangle Double carré
(ou
triangle barlong) est
isocèle et possède un côté de longueur 1. De plus il
doit s'inscrire dans un double carré.
On rencontre ce
type de triangle dans tout
l'art roman, grec et égyptien. Du fait du double carré, sa
conception est très facile.
Si sa base vaut 1, chaque
côté a pour longueur :
 |

|
La suite page suivante
 |
|
|



